Aayaan Sahu
SEARCH
Tags
LINKS
Purpose
An activation function is simply a function that is applied to the output of a node after all of the initial calculations take place. But why do we need activation functions? Without activation functions, any neural network we coneive would be a linear function, which is not very useful when we use neural networks to model complex relationships. Activation functions allow us to add non-linearity to our neural network, with a very simple change.
Recap
Recall that we could find the value of one node by summing the products of the weights and values of the nodes of the previous layers, and then adding the bias. Which can be represented by the following equation:
where is the number of nodes in the previous layers, and are the weights and values of the node, and is the bias of the node. Now, all we need to do is to apply an activation function. Let's take a look at a few.
Activation Functions
There are many activation functions, but they all have the same purpose: to add non-linearity to our neural network. Let's take a look at a few simple and popular action functions.
ReLU
ReLU stands for Rectified Linear Unit, and is the most popular activation function. It is defined as follows:
This function is very simple, and is very easy to implement. Essentially, it returns its input if it is positive, and 0 if the output is negative. In the last post, covering weights and biases, we saw that the value for one node in a hidden layer was
Applying the ReLU activation function to this value would give us . With ReLU as the activation function, the output of this node would be . This still seems quite linear because the output is the same as the input. However, the real non-linearity comes from the fact that the output is 0 if the input is negative. Let's pretend that a certain node within our neural network had a value of . Applying the ReLU activation function to this node we would receive . The graph of the ReLU activation function is as shown below.
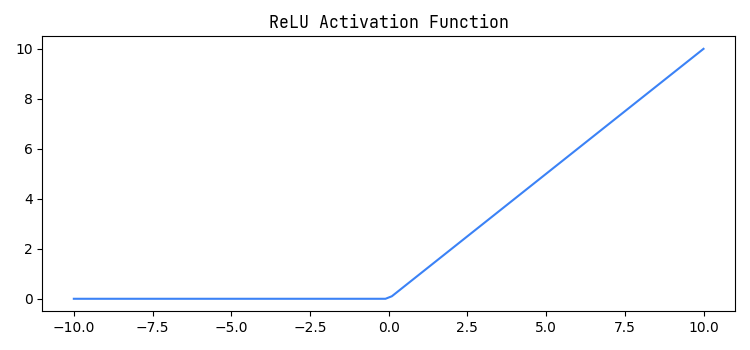
Fig 1: ReLU activation function
Sigmoid
The sigmoid activation function is defined as:
The sigmoid activation function is another very popular activation function. It maps any real number it receives as an input to a value between 0 and 1. The sigmoid activation function tends to be used in classification machine learning problems, due to the fact that the output of the sigmoid function is between 0 and 1 and can be interpreted as a probability. The graph of the sigmoid function is shown below.
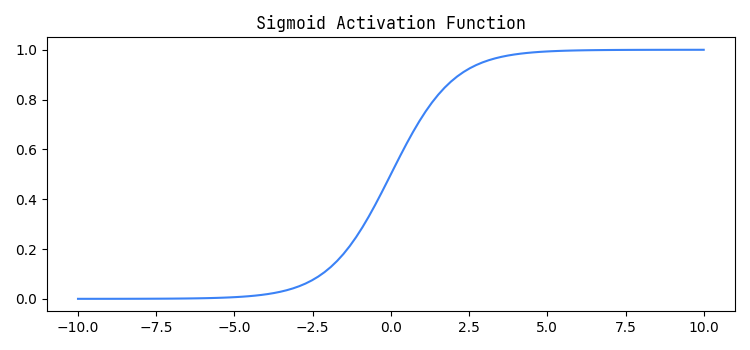
Fig 2: Sigmoid activation function
Continuing our example from the last post, we can see that the value of the node in the hidden layer is . Applying the sigmoid activation function to this value would give us . We can see the non-linearity this adds to our neural network.
Keywords
- ACTIVATION FUNCTION: The basic unit of a neural network.